|
Classes |
| struct | BoxFiller |
| | Helpers for Boxtree::Boxtree. More...
|
| struct | compElemByCenter |
| | Compare two elemntary boxes by the center point along one axis. More...
|
| struct | compElemByMin |
| | Compare two elemntary boxes by the center point along one axis. More...
|
| class | Boxtree |
| class | BoxtreePrecomp |
| | Contains all things that can be precomputed before a traversal of Boxtree's. More...
|
| class | ElemBox |
| | Elementary box, enclosing one polygon, for Boxtree. More...
|
| class | ConvexHull |
| struct | SepPlane |
| struct | DopFiller |
| struct | Dop |
| | A DOP is represented by NumOri (=k) many plane offsets. More...
|
| struct | ElemDop |
| | Elementary DOP enclosing one polygon. More...
|
| struct | DopTransform |
| | Affine transformation for DOP re-alignment. More...
|
| struct | DopNode |
| | DOP node of the DOP hierarchy. More...
|
| class | DopTree |
| class | XCollision |
| | Exceptions for Collision detection module. More...
|
| class | XQueueTooMany |
| class | XQueueNoLock |
| class | XDopTree |
| | Will be raised by DopTree. More...
|
| class | XColBug |
| | Will be raised by collision detection module, if a bug occurs somewhere in the code. More...
|
| class | XBoxtree |
| | Will be raised by BoxTree. More...
|
| class | Grid |
| struct | GridObjLtstr |
| class | GridCell |
| class | GridObj |
| class | VtableTest_Pnt3f |
| class | VtableTest_Vec3f |
| class | VtableTest1 |
| class | VtableTest2 |
| struct | Callback |
| | This is a functor for collision callbacks. More...
|
| struct | PolygonIntersectionData |
| struct | Data |
| | Holds results from collision detection and client data. More...
|
| class | CollisionPipeline |
| | This implements the whole collision detection pipeline, from front-end over broad-phase(s) to narrow-phase. More...
|
| struct | SyncFun |
| | This is a functor for synchronization with other threads. More...
|
| class | ColObj |
| | One collidable object. More...
|
| class | ColPair |
| | Pairs of ColPObjs's. More...
|
| class | MatrixCell |
| | A single cell of the collision interest matrix. More...
|
| class | Matrix |
| | The collision interest matrix. More...
|
| struct | ColPipelineData |
| | Struct to store some things which are used in Collision Detection Pipeline. More...
|
| class | Queue |
| struct | Request |
| | Each request from the application is encapsulated by an instance of this class. More...
|
| struct | EquivPoint |
| struct | TopoFace |
| | A face is a sorted array of indices into some vertrex array. More...
|
| class | Topology |
| | Zur Beschreibung von Inzidenz- und Adjazenz-Relationen. More...
|
| class | VertexIterator |
| struct | lessByAngle |
| | Compare points by angle. More...
|
| struct | sBF |
| | contains some state across different invocations of addFace() More...
|
| class | NanoTimer |
| | Timer with nanoseconds resolution. More...
|
| class | FibRand |
| | Lagged Fibonacci random sequence. More...
|
| class | VisDebug |
Typedefs |
typedef std::vector< const
DopNode * > | DopNodeList |
| typedef bool(*) | PolyIntersectT (Data *data) |
| | User-provided function for intersecting a pair of polygons.
|
Enumerations |
| enum | LevelOfDetectionE { LEVEL_BOX,
LEVEL_HULL,
LEVEL_EXACT
} |
| | Detection levels for Callback.
|
| enum | AlgoE { ALGO_DEFAULT,
ALGO_DOPTREE,
ALGO_BOXTREE
} |
| | Algorithm to apply for rigid collision detection. More...
|
| enum | RequestE {
ADD_OBJECT,
ADD_CALLBACK,
REMOVE_CALLBACK,
ACTIVATE_OBJECT,
DEACTIVATE_OBJECT,
ADD_CYCLE_CALLBACK
} |
| | The types of requests (besides check()) to the collision detection module. More...
|
Functions |
|
| BOOST_STATIC_ASSERT (Boxtree::M_MaxNVertices==4) |
| bool | intersectPolygons (const Pnt3f *poly1, int plSize1, const Pnt3f *poly2, int plSize2, const unsigned int *index1, const unsigned int *index2, const osg::Matrix *cxform) |
| | Check if two polygons intersect.
|
| bool | intersectQuadrangles (const osg::Pnt3f &polyVv0, const osg::Pnt3f &polyVv1, const osg::Pnt3f &polyVv2, const osg::Pnt3f &polyVv3, const osg::Pnt3f &polyUv0, const osg::Pnt3f &polyUv1, const osg::Pnt3f &polyUv2, const osg::Pnt3f &polyUv3, const osg::Vec3f &normal1V, const osg::Vec3f &normal2V) |
| | Checks whether two quadrangles intersect.
|
| bool | intersectTriangles (const Pnt3f &polyVv0, const Pnt3f &polyVv1, const Pnt3f &polyVv2, const Pnt3f &polyUv0, const Pnt3f &polyUv1, const Pnt3f &polyUv2) |
| | Checks if two triangles intersect.
|
| bool | intersectTriangles (const Pnt3f &polyVv0, const Pnt3f &polyVv1, const Pnt3f &polyVv2, const Pnt3f &polyUv0, const Pnt3f &polyUv1, const Pnt3f &polyUv2, const Vec3f &n1V, const Vec3f &n2V) |
| | Checks if two triangles intersect.
|
| bool | intersectCoplanarEdges (const Pnt3f &v0V, const Pnt3f &v1V, const Pnt3f &u0V, const Pnt3f &u1V, unsigned int x, unsigned int y) |
| | Checks if the edges intersect in 2D.
|
| bool | intersectEdgePolygon (const Pnt3f &v1, const Pnt3f &v2, const Pnt3f *poly, unsigned int plSize, const Vec3f &normalV, unsigned int x, unsigned int y) |
| | Checks, if edge intersects polygon.
|
|
bool | intersectEdgePolygon (const Pnt3f &v1, const Pnt3f &v2, const Pnt3f *poly, unsigned int plSize) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| bool | intersectArbPolygons (const Pnt3f *poly1, unsigned int plSize1, const Pnt3f *poly2, unsigned int plSize2, const Vec3f &normal1V, const Vec3f &normal2V) |
| | Checks if two polygons intersect.
|
|
bool | intersectArbPolygons (const Pnt3f *poly1, unsigned int plSize1, const Pnt3f *poly2, unsigned int plSize2) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
|
bool | intersectPolygons (const osg::Pnt3f *poly1, int plSize1, const osg::Pnt3f *poly2, int plSize2, const unsigned int *index1=NULL, const unsigned int *index2=NULL, const osg::Matrix *cxform=NULL) |
|
bool | intersectCoplanarTriangles (const osg::Vec3f &normalV, const osg::Pnt3f &polyVv0, const osg::Pnt3f &polyVv1, const osg::Pnt3f &polyVv2, const osg::Pnt3f &polyUv0, const osg::Pnt3f &polyUv1, const osg::Pnt3f &polyUv2) |
|
bool | intersectTriangles (const osg::Pnt3f &polyVv0, const osg::Pnt3f &polyVv1, const osg::Pnt3f &polyVv2, const osg::Pnt3f &polyUv0, const osg::Pnt3f &polyUv1, const osg::Pnt3f &polyUv2) |
|
bool | intersectTriangles (const osg::Pnt3f &polyVv0, const osg::Pnt3f &polyVv1, const osg::Pnt3f &polyVv2, const osg::Pnt3f &polyUv0, const osg::Pnt3f &polyUv1, const osg::Pnt3f &polyUv2, const osg::Vec3f &n1, const osg::Vec3f &n2) |
|
bool | intersectEdgePolygon (const osg::Pnt3f &v1, const osg::Pnt3f &v2, const osg::Pnt3f *poly, int c, const osg::Pnt3f &normalV, unsigned int x, unsigned int y) |
|
bool | intersectEdgePolygon (const osg::Pnt3f &v1, const osg::Pnt3f &v2, const osg::Pnt3f *poly, unsigned int plSize) |
|
bool | intersectArbPolygons (const osg::Pnt3f *poly1, unsigned int plSize1, const osg::Pnt3f *poly2, unsigned int plSize2) |
|
bool | intersectArbPolygons (const osg::Pnt3f *poly1, unsigned int plSize1, const osg::Pnt3f *poly2, unsigned int plSize2, const osg::Vec3f &normal1V, const osg::Vec3f &normal2V) |
|
bool | intersectCoplanarEdges (const osg::Pnt3f &v0V, const osg::Pnt3f &v1V, const osg::Pnt3f &u0V, const osg::Pnt3f &u1V, unsigned int x, unsigned int y) |
|
| BOOST_STATIC_ASSERT (sizeof(VtableTest1)==sizeof(VtableTest2)) |
|
| BOOST_STATIC_ASSERT (sizeof(osg::Pnt3f)!=sizeof(VtableTest_Pnt3f)) |
|
| BOOST_STATIC_ASSERT (sizeof(osg::Vec3f)!=sizeof(VtableTest_Vec3f)) |
|
float | operator * (const Vec4f &vec4, const Pnt3f &pnt3) |
|
Pnt3f | barycenter (const MFPnt3f *points, const unsigned int index[], const unsigned int nindices) |
|
void | getNodeBBox (NodePtr node, float min[3], float max[3]) |
|
GeometryPtr | getGeom (const NodePtr node) |
|
MFPnt3f * | getPoints (const NodePtr node) |
|
MFPnt3f * | getPoints (const GeometryPtr geo) |
|
void | mergeGeom (const NodePtr &subtree, NodePtr *geonode) |
|
void | mlerp (osg::Matrix *intermat, const osg::Matrix &m1, const osg::Matrix &m2, float t) |
|
unsigned int | sign (double &x) |
|
unsigned int | sign (int x) |
|
|
|
void | fillDops (const osg::NodePtr &node, const osg::GeometryPtr &geo, const osg::FaceIterator &fi, void *data) |
|
| float | operator * (const Vec3f &vec3, const Vec4f &vec4) |
| | Several 'vector * vector' and 'vector * point' products.
|
| float | operator * (const Pnt3f &pnt, const float vec[3]) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
|
float | operator * (const osg::Vec4f &vec4, const Pnt3f &pnt3) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
|
float | operator * (const Pnt3f &pnt3, const Vec3f &vec3) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| void | operator+= (Vec4f &vec4, const Vec3f &vec3) |
| | Vec4f += Vec3f.
|
| Pnt3f | lincomb (float c1, const Pnt3f &pnt1, float c2, const Pnt3f &pnt2) |
| | Affine combination of two points.
|
| void | getTransfomUpto (const osg::NodePtr &cur, const osg::NodePtr &upto, osg::Matrix &result) |
| | Combine all transformation matrices between two nodes in the graph.
|
| void | iterFaces (const osg::NodePtr &node, void(*callback)(const osg::NodePtr &, const osg::GeometryPtr &, const osg::FaceIterator &, void *), void *data) |
| | Calls a function for every face in the scenegraph.
|
| void | countFaces (const osg::NodePtr &, const osg::GeometryPtr &, const osg::FaceIterator &, void *data) |
| | Count the number of faces in a scenegraph.
|
| float | dist2 (const Pnt3f &pnt1, const Pnt3f &pnt2) |
| | Square distance between 2 points.
|
| float | dist (const Pnt3f &pnt1, const Pnt3f &pnt2) |
| | Distance between 2 points.
|
| Pnt3f | barycenter (const Pnt3f *points, const unsigned int npoints) |
| | Average of an array of points.
|
|
Pnt3f | barycenter (const vector< Pnt3f > &points) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| Pnt3f | barycenter (const Pnt3f *points, const unsigned int index[], const unsigned int nindices) |
| | Average of an array of indexed points.
|
|
Pnt3f | barycenter (const osg::MFPnt3f *points, const unsigned int index[], const unsigned int nindices) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
|
Pnt3f | barycenter (const vector< Pnt3f > &points, const TopoFace &face) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| bool | collinear (const Vec3f &a, const Vec3f &b) |
| | Test if two vectors are collinear.
|
| bool | coplanar (const Pnt3f &p0, const Pnt3f &p1, const Pnt3f &p2, const Pnt3f &q0, const Pnt3f &q1, const Pnt3f &q2) |
| | Test if two triangles (planes / polygons) are coplanar.
|
| Vec3f | operator * (const osg::Matrix &m, const Vec3f &v) |
| | Matrix * Vec3f.
|
| Pnt3f | mulM3Pnt (const osg::Matrix &m, const Pnt3f &p) |
| | Matrix * Pnt3f.
|
|
Pnt3f | operator * (const osg::Matrix &m, const Pnt3f &p) |
| | Matrix * vector.
|
|
osg::Matrix | operator * (const osg::Matrix &m1, const osg::Matrix &m2) |
| | Matrix * matrix.
|
| Vec3f | mulMTVec (const osg::Matrix &m, const Vec3f &v) |
| | Transposed matrix * Vec3f.
|
| void | printMat (const osg::Matrix &m, FILE *file) |
| | Print a matrix.
|
| void | printPnt (const osg::Pnt3f &p, FILE *file) |
| | Print a point.
|
| void | dominantIndices (const Vec3f &v, unsigned int *x, unsigned int *y) |
| | Dominant coord plane which v is "most orthogonal" to.
|
| void | dominantIndices (const Vec3f &v, unsigned int *x, unsigned int *y, unsigned int *z) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| unsigned int | dominantIndex (const Vec3f &v) |
| | Dominant coord axis which v is "most parallel" to.
|
| Vec3f | triangleNormal (const Pnt3f &p0, const Pnt3f &p1, const Pnt3f &p2) |
| | Normal of a triangle defined by 3 points.
|
| osg::Matrix | axisToMat (const Vec3f &a, float d) |
| | Convert a rotation given by axis & angle to a matrix.
|
| unsigned int | discretizeOri (osg::Quaternion q, unsigned int r) |
| | Convert an orientation (quarternion) into an integer (e.g., index).
|
| void | mlerp (OSG::Matrix *intermat, const OSG::Matrix &m1, const OSG::Matrix &m2, float t) |
| | Matrix linear interpolation.
|
|
| void | sortVerticesCounterClockwise (const vector< Pnt3f > &vertex, const Vec3f &normal, TopoFace &face) |
| | Sort vertices of a face such that they occur counter clockwise.
|
| osg::NodePtr | geomFromPoints (const vector< Pnt3f > &vertex, vector< TopoFace > &face, int gl_type, bool skip_redundant, const Vec3f normals[]) |
| | Create a polyhedron from simple vertex and face arrays.
|
| osg::NodePtr | geomFromPoints (const Pnt3f vertex[], unsigned int nvertices, unsigned int face[], const unsigned int face_nv[], unsigned int nfaces, int gl_type, bool skip_redundant, const Vec3f normals[]) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| osg::NodePtr | makeCube (float radius, int gl_type) |
| | Create a cube as OpenSG object.
|
| void | getNodeBBox (osg::NodePtr node, float min[3], float max[3]) |
| | Get BoundingBox of an osg-node.
|
| osg::GeometryPtr | getGeom (const osg::NodePtr node) |
| | Return the pointer to the geometry core of the node.
|
| osg::MFPnt3f * | getPoints (const osg::NodePtr node) |
| | Return the pointer to the multi-field of the points.
|
|
osg::MFPnt3f * | getPoints (const osg::GeometryPtr geo) |
| | This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
| osg::GeoPositions3fPtr | getPositions (const osg::NodePtr node) |
| | Return the GeoPositionsPtr of a node.
|
| void | calcVertexNormals (const osg::NodePtr node, const float creaseAngle) |
| | Calculate vertex normals for all geometries in a subtree.
|
| osg::NodePtr | findGeomNode (const osg::NodePtr node) |
| | Find the first node that has a geometry.
|
| osg::MaterialPtr | findMaterial (const osg::NodePtr node) |
| | Return the material a geometry node is being drawn with.
|
| void | addFace (const osg::NodePtr &node, const osg::GeometryPtr &geo, const osg::FaceIterator &face, sBF *bf) |
| | Add one face to a geometry/node; used by addAllFaces.
|
| void | addAllFaces (const osg::NodePtr &root, sBF *bf) |
| | Copy all faces in the subtree into one geometry; used by mergeGeom().
|
| void | mergeGeom (const osg::NodePtr &subtree, osg::NodePtr *geonode) |
| | Merge all geometries in a subtree into a node.
|
|
| void | sleep (unsigned int microseconds) |
| | Sleep n microseconds.
|
| float | time (void) |
| | Get the user time in milliseconds.
|
|
| double | my_drand48 (void) |
| | Substitute for the drand48() function under Unix (needed under Windoze).
|
| unsigned int | pseudo_random (void) |
| | Pseudo random number generator.
|
| float | pseudo_randomf (void) |
| | Pseudo random number generator.
|
|
| unsigned int | sign (float &x) |
| | Returns 0 if x < 0, 0x80000000 otherwise.
|
|
| bool | lockToProcessor (unsigned int processor) |
| | Lock the calling process to a certain processor.
|
|
| bool | isectCoplanarTriangles (const Vec3f &normalV, const Pnt3f &polyVv0, const Pnt3f &polyVv1, const Pnt3f &polyVv2, const Pnt3f &polyUv0, const Pnt3f &polyUv1, const Pnt3f &polyUv2) |
| | Checks whether two coplanar triangles intersect.
|
| bool | isectCoplanarEdges (const Pnt3f &v0V, const Pnt3f &v1V, const Pnt3f &u0V, const Pnt3f &u1V, unsigned int x, unsigned int y) |
| | Checks if the edges intersect in 2D.
|
| void | isectEdgePolygon (const Pnt3f &v1, const Pnt3f &v2, const Pnt3f *poly, unsigned int plSize, const Vec3f &normalV, unsigned int x, unsigned int y, bool *isect, bool *oneside) |
| | Checks, if edge intersects polygon in 2D.
|
|
void | isectEdgeTriangle (const Pnt3f &v1, const Pnt3f &v2, const Pnt3f *poly, const Vec3f &normalV, unsigned int x, unsigned int y, bool *isect, bool *oneside) |
| bool | pointInPolygon (const Pnt3f &pt, const Pnt3f *poly, unsigned int plSize, unsigned int x, unsigned int y) |
| | Check if point is inside polygon.
|
| bool | pointInTriangle (const Pnt3f &pt, const Pnt3f &v0, const Pnt3f &v1, const Pnt3f &v2, unsigned int x, unsigned int y) |
| | Check whether point is inside triangle.
|
Variables |
|
const float | M_InitEta = 0.1 |
| | Some constants for the separating planes algo ConvexHull::check(); optimal values determined by experiments.
|
|
const float | M_MaxSteps = 150 |
|
const float | M_AnnealingFactor = 0.97 |
|
int | vvv |
| const unsigned int | MaxNVertices = 10 |
| | Maximal number of vertices a polygon is allowed to contain.
|
|
const float | NearZero = 1E-6 |
| | Epsilon; all collision detection math will use this threshold.
|
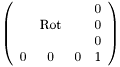 (Source: W. Schindler)
(Source: W. Schindler)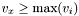 .
. 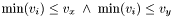 .
.
 1.5.2
1.5.2